시간복잡도와 공간복잡도

알고리즘과 데이터 구조의 효율성을 분석 및 평가에 사용되는 두가지 척도

• 점진적 표기법의 구성

  • 최상의 경우 : Big-Ω Notation (오메가표기법)
  • 평균의 경우 : Big-⍬ Notation (세타표기법)
  • 최악의 경우 : Big-Notation(빅오표기법)

• Big-O 표기법은 최악의 경우를 고려하여야 한다.

  • '’이 것 이상으로 X “ / “이 정도 까지 O” => 예측이 쉬워짐

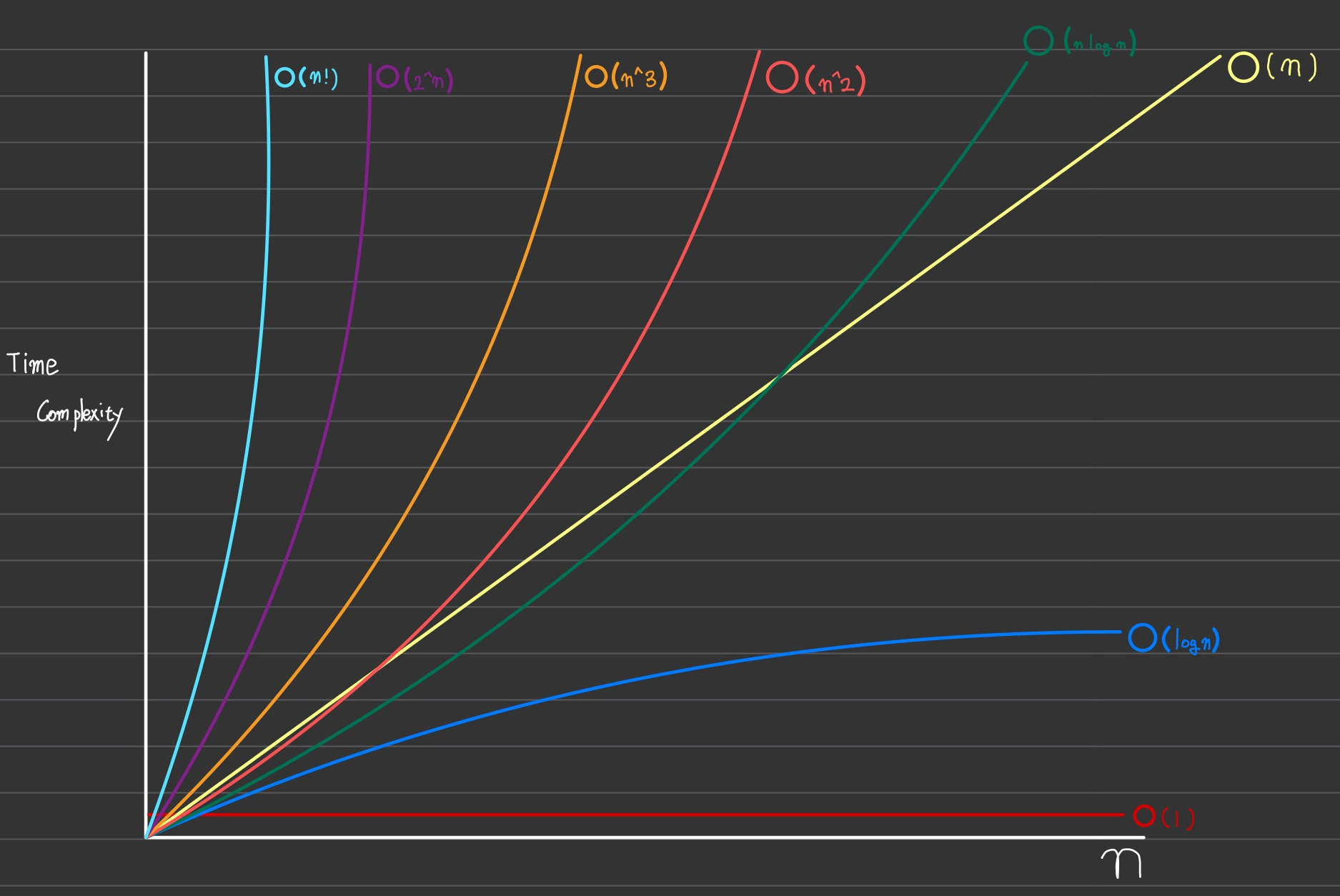
• Big-O는 복잡도 순서

  O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3, ) < O(2^n) < O(n!) 순서로 복잡도가 증가한다.

• 시∙공 간 은 Big-O 표기법으로 표기할 수 있다.

---

시간 복잡도 (Time complexity)

알고리즘의 입력 크기의 함수로 실행하는 데 걸리는 시간을 뜻함

---

O(1) Constant complexity (일정한 복잡도)

• 입력한 값이 증가하더라도 시간이 늘지 않는다.
• 입력값이 아무리 크더라도 즉시 출력값을 얻어낼 수 있다.

  # 두개의 숫자 더하기 #
  function add(a,b) {
    return a + b
  }
  

  # 배열의 특정 요소 접근 #
  const array = [1, 2, 3, 4, 5]
  console.log (array[3]) // 4
  

  # 문자열 길이 측정 #
  const length = "Hello Time Complexity"
  console.log (length.length) // 21
  

---

O(log n) logarithmic complexity (로그 복잡도)

• 입력 크기가 커짐에 따라 걸리는 시간이 천천히 증가
• 그래프는 n이 증가함에 따라 낮게 시작하여 상승하고 평평해지는 곡선을 갖게 됨
• 이는 이진 검색(binary Search) 알고리즘에서 일반적

  # 바이너리(이진)검색
  function binarySearch(array, target) { // 검색범위의 하한 및 상한을 각각 배열의 첫 번째 인덱스와 마지막 인덱스로 초기화
    let low = 0 // 하한
    let high = array.length -1 // 상한
  
    while (low <= high) {
        let mid = math.floor((low + high)/2) // 나누기를 통해 검색범위의 중간을 계산
        if (array[mid] === target) { // 타겟과 대상이 같은지 판단
            return mid // 같다면 mid를 반환
        } else if (array[mid] < target) { // 대상이 타겟보다 작다면
            low = mid + 1 // 하한에 1을 더하고 그 대상요소의 위쪽을 검색한다.
        } else if (array[mid] > target) { // 대상이 타겟보다 크다면
            high = mid - 1 // 상한에 1을 빼고 그 대상요소의 아랫쪽을 검색한다.
        }
    }
    return -1 // 대상 요소가 없다면 -1 을 반환
  }
  

---

O(n) Linear complexity (선형 복잡도)

• 시간은 입력 크기에 비례하여 증가합니다.
• 그래프는 입력 크기와 걸린 시간 사이의 1:1 관계를 나타내는 양의 기울기가 있는 직선
• 선형 시간 복잡도 알고리즘의 예로는 단순 검색 및 순회 알고리즘

  function findMaxIndex(array){ // array를 인자로 받음
    let maxIndex = 0 // 최대값 index를 maxIndex라 하고 0 으로 초기화
    for (let i = 1; i < array.length; i++) { // for 반복문을 통해 배열의 길이만큰 탐색
        if (array[i] > array[maxIndex]) { // 탐색한 index가 maxIndex 보다 클 경우 
            maxIndex = i // 탐색 index로 업데이트
        }
    }
    return maxIndex // 탐색이 끝나면 maxIndex 반환
  }
  # Index의 크기가 증가 할 수록 탐색시간이 증가
  

---

O(n log n) Linearithmic complexity (선형 복잡도)

• 선형과 2차 사이의 성장률을 나타냄
• 그래프는 낮게 시작하여 n이 커짐에 따라 기울기가 점차 증가하는 곡선
• 이는 병합 정렬 및 퀵 정렬과 같은 정렬 알고리즘에 일반적

병합정렬 알고리즘

function mergeSort(array) {
	if (array.length <= 1) { // 병합정렬 (mergeSort) 함수는 배열을 입력으로 사용하고 배열의 정렬된 버전을 반환 배열의 길이가 1 또는 0 이면, 이미 정렬된 것으로 함수는 변경되지 않고 반환 됨
		return array
	}
	const midIndex = Math.floor(array.length / 2) // 반환되지 않으면 배열을 나누어 중간 인덱스를 할당
	const leftIndex = array.slice(0,midIndex) // 왼쪽 정렬
	const rightIndex = array.slice(midIndex) // 오른쪽 정렬

	const sortedLeftArray = mergeSort(leftArray) // 왼쪽 정렬 mergeSort 이용 재귀적 정렬
	const sortedRightArray = mergeSort(rightIndex) // 오른쪽 정렬 mergeSort 이용 재귀적 정렬

	return mergre(sortedLeftArray, sortedRightArray) //merge로 병합하여 정렬된 배열이 반환 됨
}

병합 알고리즘
function merge(leftArray, rightArray) { // 3가지 leftIndex, rightIndex, mergeArray 초기화
	let leftIndex = 0
	let rightIndex = 0
	let mergeArray = []

	while (leftIndex < leftArray.length && rightIndex < rightArray.length) {
	// 이 함수는 왼쪽 및 오른쪽 배열을 비교하고 각 단계에서 병합된 배열에 가장 작은 값을 추가하는 while 루프를 사용하여 배열을 반복
		if (leftArray[leftIndex] < rightArray[rightIndex]) {
			mergeArray.push(leftArray[leftIndex])
			leftIndex++
		} else {
			mergeArray.push(rightArray[rightIndex])
			rightIndex++
		}
	}
  // 배열 중 하나가 소진되면 함수는 다른 배열의 나머지 요소를 병합된 배열에 추가
	while (leftIndex < leftArray.length) {
		mergeArray.push(leftArray[leftIndex])
		leftIndex++
	}
	while (rightIndex < rightArray.length) {
		mergeArray.push(rightArray[rightIndex])
		rightIndex++
	}
	// 병합된 배열이 반환됩니다.
	return mergedArray;
}

---

O(n^2) Quadratic complexity (2차 복잡도)

• 소요 시간은 입력 크기의 제곱에 따라 증가
• 그래프는 낮게 시작하여 n이 증가함에 따라 기울어지는 포물선 곡선
• 버블 정렬 및 삽입 정렬과 같은 중첩 루프 알고리즘의 특징

  function sumOfPairs(array) { 
    let sum = 0; 
    for (let i = 0; i < array.length; i++) { 
        for (let j = i + 1; j < array.length; j++) { 
        sum += array[i] + array[j]; 	
        } 
    } 
    return sum; 
  } 
  const array = [1, 2, 3, 4]; 
  console.log(sumOfPairs(array)); // Output: 20
  

---

O(n^3) Cubic complexity (큐빅 복잡도)

• 입력 크기의 세제곱에 비례하는 성장률을 나타냄
• 그래프는 낮게 시작하여 급격히 가팔라지고 n이 증가함에 따라 계속 가파르게 되는 곡선을 갖게 됨
• 3개의 중첩 루프가 있는 알고리즘에서 일반적

  function productOfTriplets(array) {
  let product = 1;
  
  for (let i = 0; i < array.length; i++) {
    for (let j = i + 1; j < array.length; j++) {
      for (let k = j + 1; k < array.length; k++) {
        product *= array[i] * array[j] * array[k];
      }
    }
  }
  return product;
  }
  const array = [1, 2, 3, 4];
  console.log(productOfTriplets(array)); // Output: 144
  

---

O(2^n) Exponential complexity (지수적 복잡도)

• 기하급수적으로 복잡한 알고리즘의 경우 입력 크기가 증가할 때마다 걸리는 시간이 두 배가 됨
• 그래프는 n이 커짐에 따라 거의 수직이 되는 가파른 곡선을 보여줌
• 방문 판매원 문제에 대한 무차별 대입 솔루션과 같은 일부 재귀 알고리즘에서 일반적

  function generateSubsets(set) {
  const subsets = [];
  for (let i = 0; i < Math.pow(2, set.length); i++) {
    const subset = [];
    for (let j = 0; j < set.length; j++) {
      if (i & (1 << j)) {
        subset.push(set[j]);
      }
    }
    subsets.push(subset);
  }
  return subsets;
  }
  const set = [1, 2, 3];
  console.log(generateSubsets(set)); // Output: [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
  

---

O(n!) Factorial complexity (계승 복잡도)

• n이 커질수록 알고리즘을 완료하는 데 필요한 작업 수가 매우 빠르게 증가하므로 대부분의 실제 응용 프로그램에서는 비실용적

  function generatePermutations(set) {
  const permutations = [];
  
  function swap(array, i, j) {
    const temp = array[i];
    array[i] = array[j];
    array[j] = temp;
  }
  function permute(array, startIndex) {
    if (startIndex === array.length - 1) {
      permutations.push([...array]);
    } else {
      for (let i = startIndex; i < array.length; i++) {
        swap(array, startIndex, i);
        permute(array, startIndex + 1);
        swap(array, startIndex, i);
      }
    }
  }
  permute(set, 0);
  return permutations;
  }
  const set = [1, 2, 3];
  console.log(generatePermutations(set)); // Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,2,1],[3,1,2]]
  

---

공간 복잡도 (Space Complexity)

알고리즘이 입력 크기의 함수로 문제를 해결하기위해 사용하는 메모리양

• 프로그램을 실행 및 완료하는데 필요한 저장공간의 양
• 총 필요 저장 공간
  • 고정공간 (알고리즘과 무관한 공간) : 코드 저장공간, 단순 변수 및 상수
  • 가변공간 (알고리즘 실행과 관련있는 공간) : 실행 중 동적으로 필요한 공간
  • S(P) = c + Sp(n)
    • c : 고정공간
    • Sp(n) : 가변공간

고정공간은 상수 이므로, 공간 복잡도는 가변 (Sp(n))에 영향을 받음

O(1) Constant complexity (일정한 복잡도)

function exampleFunction() {
	const a = 1;
	const b = 2;
	const c = 3;
	return a + b + c;
}

console.log(`Memory usage: ${memoryUsage} bytes`); // output 1720 Bytes

---

O(log n) logarithmic complexity (로그 복잡도)

// Define an O(log n) space complexity function

function exampleFunction(n) {
	let result = 0;
	for (let i = 1; i <= n; i *= 2) {
		result += i;
	}
	return result;
}

const memoryUsageBefore = process.memoryUsage().heapUsed;
exampleFunction(n);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore

console.log(`Memory usage: ${memoryUsage} bytes`); // exampleFunction(1000 ~ 1000000000) => output : 1720 Bytes
																									 // exampleFunction(10000000000) => output : 1832 Bytes

---

O(n) Linear complexity (선형 복잡도)

// Define an O(log n) space complexity function
function exampleFunction(n) {
	const array = [];
	for (let i = 0; i < n; i++) {
		array.push(i);
	}
	return array;
}
const memoryUsageBefore = process.memoryUsage().heapUsed;
exampleFunction(10);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore;

console.log(`N(${n})일 때, Memory usage: ${memoryUsage} bytes`);
N(10)일 때, Memory usage: 1904 bytes
N(100)일 때, Memory usage: 4072 bytes
N(1000)일 때, Memory usage: 30360 bytes
N(10000)일 때, Memory usage: 247112 bytes

---

O(n log n) Linearithmic complexity (선형 복잡도)

// Define an O(n log n) space complexity function
function exampleFunction(n) {
	const array = [];
	for (let i = 0; i < n; i++) {
		array.push(Math.floor(Math.random() * n));
	}
	array.sort();
	return array;
}
const memoryUsageBefore = process.memoryUsage().heapUsed;
let n = 10;
exampleFunction(n);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore;

console.log(`N(${n})일 때, Memory usage: ${memoryUsage} bytes`);
N(10)일 때, Memory usage: 3152 bytes
N(100)일 때, Memory usage: 9312 bytes
N(1000)일 때, Memory usage: 85584 bytes
N(10000)일 때, Memory usage: 731496 bytes

---

O(n^2) Quadratic complexity (2차 복잡도)

// Define an O(n^2) space complexity function
function exampleFunction(n) {
	const matrix = [];
	for (let i = 0; i < n; i++) {
		matrix[i] = [];
		for (let j = 0; j < n; j++) {
			matrix[i][j] = i * j;
		}
	}
	return matrix;
}
const memoryUsageBefore = process.memoryUsage().heapUsed;
let n = 10;
exampleFunction(n);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore;

console.log(`N(${n})일 때, Memory usage: ${memoryUsage} bytes`);

N(10)일 때, Memory usage: 3872 bytes
N(100)일 때, Memory usage: 241680 bytes
N(1000)일 때, Memory usage: 13584624 bytes
N(10000)일 때, Memory usage: 807010848 bytes

---

O(n^3) Cubic complexity (큐빅 복잡도)

// Define an O(n^3) space complexity function
function exampleFunction(n) {
	const matrix = [];
	for (let i = 0; i < n; i++) {
		matrix[i] = [];
		for (let j = 0; j < n; j++) {
			matrix[i][j] = [];
			for (let k = 0; k < n; k++) {
				matrix[i][j][k] = i * j * k;
			}
		}
	}
	return matrix;
}

const memoryUsageBefore = process.memoryUsage().heapUsed;
let n = 10;
exampleFunction(n);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore;

console.log(`N(${n})일 때, Memory usage: ${memoryUsage} bytes`);
N(10)일 때, Memory usage: 23904 bytes
N(100)일 때, Memory usage: 13620472 bytes
N(500)일 때, Memory usage: 1124227816 bytes
N(1000)일 때, heap Memory 초과 

---

O(2^n) Exponential complexity (지수적 복잡도)

// Define an O(2^n) space complexity function
function exampleFunction(n) {
	if (n === 0) {
		return [[]];
	} else {
		const prev = exampleFunction(n - 1);
		const result = [];
		for (let i = 0; i < prev.length; i++) {
			result.push([...prev[i], 0]);
			result.push([...prev[i], 1]);
		}
		return result;
	}
}

const memoryUsageBefore = process.memoryUsage().heapUsed;
let n = 10;
exampleFunction(n);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore;

console.log(`N(${n})일 때, Memory usage: ${memoryUsage} bytes`);
N(10)일 때, Memory usage: 796552 bytes
N(20)일 때, Memory usage: 791310504 bytes
N(21)일 때, Memory usage: 1401836816 bytes
N(22)일 때, Memory usage: 2818895488 bytes
N(23)일 때, heap Memory 초과

---

O(n!) Factorial complexity (계승 복잡도)

function exampleFunction(n) {
  if (n <= 1) {
    return [[n]];
  } else {
    const prev = eexampleFunction(n - 1);
    const result = [];
    for (let i = 0; i < prev.length; i++) {
      for (let j = 0; j < n; j++) {
        const copy = [...prev[i]];
        copy.splice(j, 0, n);
        result.push(copy);
      }
    }
    return result;
  }
}

const memoryUsageBefore = process.memoryUsage().heapUsed;
let n = 10;
exampleFunction(n);
const memoryUsageAfter = process.memoryUsage().heapUsed;
const memoryUsage = memoryUsageAfter - memoryUsageBefore;  

console.log(`N(${n})일 때, Memory usage: ${memoryUsage} bytes`);
N(10)일 때, Memory usage: 1254587888 bytes
N(11)일 때, heap memory 초과